Solving a multi-objective solid transportation problem: a comparative study of alternative methods for decision-making

Abstract

The transportation problem in operations research aims to minimize costs by optimizing the allocation of goods from multiple sources to destinations, considering supply, demand, and transportation constraints. This paper applies the multi-dimensional solid transportation problem approach to a private sector company in Egypt, aiming to determine the ideal allocation of their truck fleet.

In order to provide decision-makers with a comprehensive set of options to reduce fuel consumption costs during transportation or minimize total transportation time, a multi-objective approach is employed. The study explores the best compromise solution by leveraging three multi-objective approaches: the Zimmermann Programming Technique, Global Criteria Method, and Minimum Distance Method. Optimal solutions are derived for time and fuel consumption objectives, offering decision-makers a broad range to make informed decisions for the company and the flexibility to adapt them as needed.

Lingo codes are developed to facilitate the identification of the best compromise solution using different methods. Furthermore, non-dominated extreme points are established based on the weights assigned to the different objectives. This approach expands the potential ranges for enhancing the transfer problem, yielding more comprehensive solutions.

This research contributes to the field by addressing the transportation problem practically and applying a multi-objective approach to support decision-making. The findings provide valuable insights for optimizing the distribution of the truck fleet, reducing fuel consumption costs, and improving overall transportation efficiency.

Introduction

The field of operations research has identified the transportation problem as an optimization issue of significant interest [1, 2]. This problem concerns determining the optimal approach to allocate a given set of goods that come from particular sources to the designated destinations to minimize the overall transportation costs [3]. The transportation problem finds applications in various areas, including logistics planning, distribution network design, and supply chain management. Solving this problem relies on the assumption that the supply and demand of goods are known, as well as the transportation cost for each source–destination pairing [4, 5].

Solving the transportation problem means finding the right quantities of goods to be transported from the sources to the destinations, given the supply and demand restrictions. The ultimate goal is to minimize the total transportation cost, which is the sum of the cost for each shipment [6]. Various optimization algorithms have been developed for this problem, such as the North-West Corner Method, the Least Cost Method, and Vogel’s Approximation Method [7].

A solid transportation problem (STP) is a related transportation problem that centers around a single commodity, which can be stored at interim points [8]. These interim points, known as transshipment points, act as origins and destinations. The STP involves determining the most efficient means of transporting the commodity from the sources to the destinations, while minimizing transportation costs by going through the transshipment points. The STP has real-world applications in container shipping, air cargo transportation, and oil and gas pipeline transportation [9, 10].

Multi-dimensional solid transportation problem (MDSTP) represents a variation on the STP, incorporating multiple commodities that vary in properties such as volume, weight, and hazard level [11]. The MDSTP aims to identify the best way to transport each commodity from the sources to the destinations, taking into account the capacity restrictions of transshipment points and hazardous commodity regulations [12]. The MDSTP is more complex than the STP and requires specific algorithms and models for its resolution.

Solving the STP and MDSTP requires identifying the most effective routing of commodities and considering the storage capacity of transshipment points. The goal is to minimize total transportation costs while satisfying supply and demand constraints and hazardous material regulations. Solutions to these problems include the Network Simplex Method, Branch and Bound Method, and Genetic Algorithm [13]. Solving the STP and MDSTP contributes valuable insights into the design and operation of transportation systems and supports improved sustainability and efficiency.

In the field of operations research, two critical research areas are the multi-objective transportation problem (MOTP) and the multi-objective solid transportation problem (MOSTP) [14]. The MOTP aims to optimize the transportation of goods from multiple sources to various destinations by considering multiple objectives, including minimizing cost, transportation time, and environmental impacts. The MOSTP, on the other hand, focuses on the transportation of solid materials, such as minerals or ores, and involves dealing with multiple competing objectives, such as cost, time, and quality of service. These problems are essential in logistics and supply chain management, where decision-makers must make optimal transportation plans by considering multiple objectives. Researchers and practitioners often employ optimization techniques, such as mathematical programming, heuristics, and meta-heuristics, to address these challenges efficiently [15].

Efficient transportation planning is essential for moving goods from their source to the destination. This process involves booking different types of vehicles and minimizing the total transportation time and cost is a crucial factor to consider. Various challenges can affect the optimal transportation policy, such as the weight and volume of products, the availability of specific vehicles, and other uncertain parameters. In this regard, several studies have proposed different approaches to solve the problem of multi-objective solid transportation under uncertainty. One such study by Kar et al. [16] used fuzzy parameters to account for uncertain transportation costs and time, and two methods were employed to solve the problem, namely the Zimmermann Method and the Global Criteria Method.

Similarly, Mirmohseni et al. [17] proposed a fuzzy interactive probabilistic programming approach, while Kakran et al. [18] addressed a multi-objective capacitated solid transportation problem with uncertain zigzag variables. Additionally, Chen et al. [19] investigated an uncertain bicriteria solid transportation problem by using uncertainty theory properties to transform the models into deterministic equivalents, proposing two models, namely the expected value goal programming and chance-constrained goal programming models [20]. These studies have contributed to developing different approaches using fuzzy programming, uncertainty theory, and related concepts to solve multi-objective solid transportation problems with uncertain parameters.

This paper presents a case study carried out on a private sector company in Egypt intending to ascertain the minimum number of trucks required to fulfill the decision-makers’ objectives of transporting the company’s fleet of trucks from multiple sources to various destinations. This objective is complicated by the diversity of truck types and transported products, as well as the decision-makers’ multiple priorities, specifically the cost of fuel consumption and the timeliness of truck arrival.

In contrast to previous research on the transportation problem, this paper introduces a novel approach that combines the multi-dimensional solid transportation problem framework with a multi-objective optimization technique. Building upon previous studies, which often focused on single-objective solutions and overlooked specific constraints, our research critically analyzes the limitations of these approaches. We identify the need for comprehensive solutions that account for the complexities of diverse truck fleets and transported products, as well as the decision-makers’ multiple priorities. By explicitly addressing these shortcomings, our primary goal is to determine the minimum number of trucks required to fulfill the decision-makers’ objectives, while simultaneously optimizing fuel consumption and transportation timeliness. Through this novel approach, we contribute significantly to the field by advancing the understanding of the transportation problem and providing potential applications in various domains. Our research not only offers practical solutions for real-world scenarios but also demonstrates the potential for improving transportation efficiency and cost-effectiveness in other industries or contexts. The following sections will present a comparative analysis of the proposed work, highlighting the advancements and novelty introduced by our approach.

Methods/experimental

Aim

This study uses a case study from Egypt to find the optimal distribution of a private sector company’s truck fleet under various optimization and multi-objective conditions. Specifically, the study aims to optimize the distribution of a private sector company’s truck fleet by solving a multi-objective solid transportation problem (MOSTP) and comparing three different methods for decision-making.

Design and setting

This study uses a case study design in a private sector company in Egypt. The study focuses on distributing the company’s truck fleet to transport products from factories to distribution centers.

Participants or materials

The participants in this study are the transportation planners and managers of the private sector company in Egypt. The materials used in this study include data on the truck fleet, sources, destinations, and products.

Processes and methodologies

The study employs the multi-objective multi-dimensional solid transportation problem (MOMDSTP) to determine the optimal solution for the company’s truck fleet distribution, considering two competing objectives: fuel consumption cost and total shipping time. The MOMDSTP considers the number and types of trucks, sources, destinations, and products and considers the supply and demand constraints.

To solve the MOMDSTP, three decision-making methods are employed: Zimmermann Programming Technique, Global Criteria Method, and Minimum Distance Method. The first two methods directly yield the best compromise solution (BCS), whereas the last method generates non-dominated extreme points by assigning different weights to each objective. Lingo software is used to obtain the optimal solutions for fuel consumption cost and time and the BCS and solutions with different weights for both objectives.

Ethics approval and consent

This study does not involve human participants, data, or tissue, nor does it involve animals. Therefore, ethics approval and consent are not applicable.

Statistical analysis

Statistical analysis is not conducted in this study. However, the MOMDSTP model and three well-established decision-making methods are employed to derive the optimal distribution of the company’s truck fleet under various optimization and multi-objective conditions.

In summary, this study uses a case study design to find the optimal distribution of a private sector company’s truck fleet under various optimization and multi-objective conditions. The study employs the MOMDSTP and three methods for decision-making, and data on the truck fleet, sources, destinations, and products are used as materials. Ethics approval and consent are not applicable, and statistical analysis is not performed.

Multi-objective transportation problem

The multi-objective optimization problem is a complex issue that demands diverse approaches to determine the most satisfactory solution. Prevalent techniques employed in this domain include the Weighted Sum Method, Minimum Distance Method, Zimmermann Programming Technique, and Global Criteria Method. Each method offers its own benefits and limitations, and the selection of a specific method depends on the nature of the problem and the preferences of the decision-makers [21].

This section discusses various methodologies employed to identify the most optimal solution(s) for the multi-objective multi-dimensional solid transportation problem (MOMDSTP), which is utilized as the basis for the case study. These methodologies encompass the Minimum Distance Method (MDM), the Zimmermann Programming Technique, and the Global Criteria Method [22].

Zimmermann Programming Technique

The Zimmermann Programming Technique (ZPT) is a multi-objective optimization approach that was developed by Professor Hans-Joachim Zimmermann in the late 1970s. This technique addresses complex problems with multiple competing objectives that cannot be optimized simultaneously. Additionally, it incorporates the concept of an “aspiration level,” representing the minimum acceptable level for each objective. The aspiration level ensures that the solution obtained is satisfactory for each objective. If the solution does not meet the aspiration level for any objective, the weights are adjusted, and the optimization process is iterated until a satisfactory solution is obtained.

A key advantage of ZPT is its ability to incorporate decision-makers’ preferences and judgments into the decision-making process. The weights assigned to each objective are based on the decision-maker’s preferences, and the aspiration levels reflect their judgments about what constitutes an acceptable level for each objective [23].

The Zimmermann Programming Technique empowers decision-makers to incorporate multiple objectives and achieve a balanced solution. By assigning weights to objectives, a trade-off can be made to find a compromise that meets various criteria. For example, this technique can optimize cost, delivery time, and customer satisfaction in supply chain management [24]. However, the interpretation of results may require careful consideration, and computational intensity can increase with larger-scale and complex problems.

 In order to obtain the solution, each objective is considered at a time to get the lower and upper bounds for that objective. Let for objective, and are the lower (min) and upper (max) bounds. The membership functions of the first and second objective functions can be generated based on the following formula [25]:

$${\mu }_{k}\left({F}_{k}\left(x\right)\right)=\left\{\begin{array}{ccl} 1& \qquad if & \qquad {F}_{k}(x)\le {L}_{k}\\ \frac{{U}_{k}-{F}_{k}\left(x\right)}{{U}_{k}-{L}_{k}} & \qquad if & \qquad {L}_{k}<{F}_{k}(x)<{U}_{k}\\ 0 & \qquad if & \qquad {F}_{k}(x)\ge {U}_{k}\end{array}\right.$$

Next, the fuzzy linear programming problem is formulated using the max–min operator as follows:

• Maximize min ${\mu }_{k}\left({F}_{k}\left(x\right)\right)$  

• Subject to ${g}_{i}\left(x\right) \left\{ \le ,= , \ge \right\}{b}_{i}\mathrm{ where }\;i = 1, 2, 3, ..., m.$  

• Moreover, x ≥ 0.

Global Criteria Method

The Global Criteria Method is a multi-objective optimization method that aims to identify the set of ideal solutions based on predetermined criteria. This method involves defining a set of decision rules that assess the feasibility and optimality of the solutions based on the objectives and constraints [26]. By applying decision rules, solutions that fail to meet the predetermined criteria are eliminated, and the remaining solutions are ranked [27].

The Global Criteria Method assesses overall system performance, aiding decision-makers in selecting solutions that excel in all objectives. However, it may face challenges when dealing with conflicting objectives [28]. Furthermore, it has the potential to overlook specific details, and the choice of aggregation function or criteria can impact the results by favoring specific solutions or objectives.

Let us consider the following ideal solutions:

• f1* represents the ideal solution for the first objective function,

• f2* represents the ideal solution for the second objective function, and

• n1* represents the ideal solution for the nth objective function.

Objective function formula:

• Minimize the objective function F = $\sum_{k=1}^{n}{(\frac{{f}_{k}\left({x}^{*}\right)-{f}_{k}(x)}{{f}_{k}({x}^{*})})}^{p}$

• Subject to the constraints: g_i(x) $\le$ 0, i = 1, 2,.., m

• The function fk(x) can depend on variables x₁, x₂, …, x_n.

Minimum Distance Method

The Minimum Distance Method (MDM) is a novel distance-based model that utilizes the goal programming weighted method. The model aims to minimize the distances between the ideal objectives and the feasible objective space, leading to an optimal compromise solution for the multi-objective linear programming problem (MOLPP) [29]. To solve MOLPP, the proposed model breaks it down into a series of single objective subproblems, with the objectives transformed into constraints. To further enhance the compromise solution, priorities can be defined using weights, and a criterion is provided to determine the best compromise solution. A significant advantage of this approach is its ability to obtain a compromise solution without any specific preference or for various preferences.

The Minimum Distance Method prioritizes solutions that closely resemble the ideal or utopian solution, assisting decision-makers in ranking and identifying high-performing solutions. It relies on a known and achievable ideal solution, and its sensitivity to the chosen reference point can influence results. However, it does not provide a comprehensive trade-off solution, focusing solely on proximity to the ideal point [30].

The mathematical formulation for MDM for MOLP is as follows:

• The formulation for multi-objective linear programming (MOLP) based on the minimum distance method is referred to[31]. It is possible to derive the multi-objective transportation problem with two objective functions using this method and its corresponding formula.

  $$\mathrm{Minimize}\;\mathrm{the}\;\mathrm{objective}\;\mathrm{function}\;F=\left(f_1-f_1^\ast\right)\left(1-w_1\right)d+\left(f_2-f_2^\ast\right)\left(1-w_2\right)d$$

Subject to the following constraints:

$$\sum_{i=1}^{m}\sum_{j=1}^{n}{c}_{ij}^{1} {x}_{ij}^{1}\le {f}_{1}^{*}+d(1-{w}_{1})$$

$$\sum_{i=1}^{m}\sum_{j=1}^{n}{c}_{ij}^{2} {x}_{ij}^{2} \le {f}_{2}^{*}+d(1-{w}_{2})$$

$$\sum_{i=1}^{m}{x}_{ij}={a}_{i}, \qquad j=\mathrm{1,2},3,\dots ,n.$$

$$\sum_{j=1}^{n}{x}_{ij}={b}_{i}, \qquad i=\mathrm{1,2},3,\dots ,m.$$

$$w_1+w_2=1\;\mathrm{and}\;w_l\geq0;\;\mathrm{and}\;l=1,2.$$

$$x_{ij}\geq0,i=1,2,3,\dots,m\;\mathrm{and}\;j=1,2,3,\dots n.$$

where:

• f^*₁, f^*₂: the obtained ideal objective values by solving single objective STP.

• w₁, w₂: weights for objective1 and objective2 respectively.

• f1, f2: the objective values for another efficient solution.

• d: general deviational variable for all objectives.

• ${{c}_{ij}^{1}, c}_{ij}^{2}$: the unit cost for objectives 1 and 2 from source i to destination j.

• ${{x}_{ij}^{1}, x}_{ij}^{2}$: the amount to be shipped when optimizing for objectives 1 and 2 from source i to destination j.

Mathematical model for STP

The transportation problem (TP) involves finding the best method to ship a specific product from a defined set of sources to a designated set of destinations, while adhering to specific constraints. In this case, the objective function and constraint sets take into account three-dimensional characteristics instead of solely focusing on the source and destination [32]. Specifically, the TP considers various modes of transportation, such as ships, freight trains, cargo aircraft, and trucks, which can be used to represent the problem in three dimensions When considering a single mode of transportation, the TP transforms into a solid transportation problem (STP), which can be mathematically formulated as follows:

The mathematical form of the solid transportation problem is given by [33]:

$$\mathrm{Min}\; Z={{\textstyle\sum_{i=1}^m}{\textstyle\sum_{j=1}^n}{\textstyle\sum_{k=1}^p}c_{ijk}x_{ijk}}$$

Subject to:

$$\begin{array}{cc}\textstyle\sum_{j=1}^n\sum_{k=1}^px_{ijk}=a_i \qquad \qquad \text{i}=1,\;2,\;\dots,\; \text{m}\end{array}$$

$$\begin{array}{cc}\begin{array}{cc}\textstyle\sum_{i=1}^m&\textstyle\sum_{k=1}^px_{ijk}=b_j \qquad \end{array}&\text{j}=1,\;2,\;\dots, \text{n}\end{array}$$

$$\begin{array}{cc}{\textstyle\sum_{i=1}^m}{\textstyle\sum_{j=1}^n}x_{ijk}=e_k& \qquad \text{k}=1,\;2,\;\dots,\; \text{p}\end{array}$$

$$x_{ijk}\geq0\;\mathrm{for}\;\mathrm{all}\mathit\;j\mathit,\mathit\;j\mathit,\mathit\;k$$

where:

• Z = the objective function to be minimized

• m = the number of sources in the STP

• n = the number of destinations in the STP

• p = the number of different modes of transportation in the STP

• x_ijk represents the quantity of product transported from source i to destination j using conveyance k

• c_ijk = the unit transportation cost for each mode of transportation in the STP

• a_i = the amount of products available at source i

• b_j = the demand for the product at destination j

• e_k = the maximum amount of product that can be transported using conveyance k

The determination of the size of the fleet for each type of truck that is dispatched daily from each factory to all destinations for the transportation of various products is expressed formally as follows:

$$\begin{array}{cc}Z_{\mathrm{ik}}=\left({\textstyle\sum_{\mathrm j\in\mathrm J}\sum_{\mathrm p\in\mathrm P}\;\;x_{ijkp}}\right)/{\mathrm C}_{\mathrm k}& \qquad \mathrm{for}\;\forall\;\text{k}\mathit=1:\mathrm K;\; \qquad \text{i}\end{array}=1:\mathrm I$$

where:

• z_ik denotes the number of trucks of type k that are dispatched daily from factory i.

• C_k represents the capacity of truck k in terms of the number of pallets it can transport.

• x_ijk denotes a binary decision variable that is set to one if truck k is dispatched from factory i to destination j to transport product p, and zero otherwise. The summation is performed over all destinations j and all products p.

Case study

This case study focuses on an Egyptian manufacturing company that produces over 70,000 pallets of various water and carbonated products daily. The company has 25 main distribution centers and eight factories located in different industrial cities in Egypt. The company’s transportation fleet consists of hundreds of trucks with varying capacities that are used to transport products from factories to distribution centers. The trucks have been classified into three types (type A, type B, and type C) based on their capacities. The company produces three different types of products that are packaged in pallets. It was observed that the sizes and weights of the pallets are consistent across all product types The main objective of this case study is to determine the minimum number of each truck type required in the manufacturer’s garage to minimize fuel consumption costs and reduce product delivery time.

The problem was addressed by analyzing the benefits of diversifying trucks and implementing the solid transport method. Subsequently, the problem was resolved while considering the capacities of the sources and the requirements of the destinations. The scenario involved shipping products using a single type of truck, and the fuel consumption costs were calculated accordingly. The first objective was to reduce the cost of fuel consumption on the one-way journey from the factories to the distribution centers. The second objective was to reduce the time of arrival of the products to the destinations. The time was calculated based on the average speed of the trucks in the company’s records, which varies depending on the weight and size of the transported goods.

To address the multiple objectives and the uncertainty in supply and demand, an approach was adopted to determine the minimum number of trucks required at each factory. This approach involved determining the maximum number of trucks of each type that should be present in each factory under all previous conditions. The study emphasizes the significance of achieving a balance between reducing transportation costs and time while ensuring trucks are capable of accommodating quantities of any size, thus avoiding underutilization.

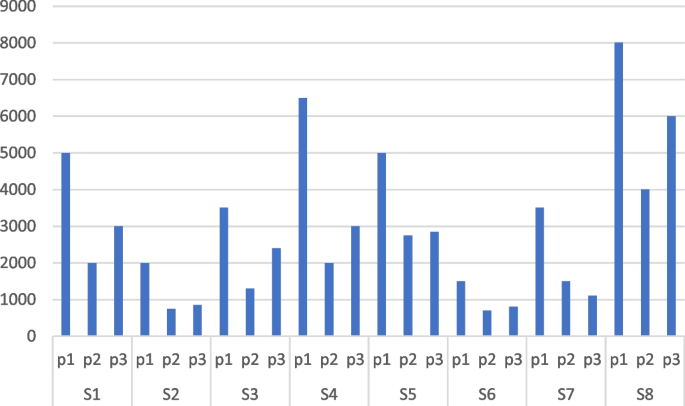
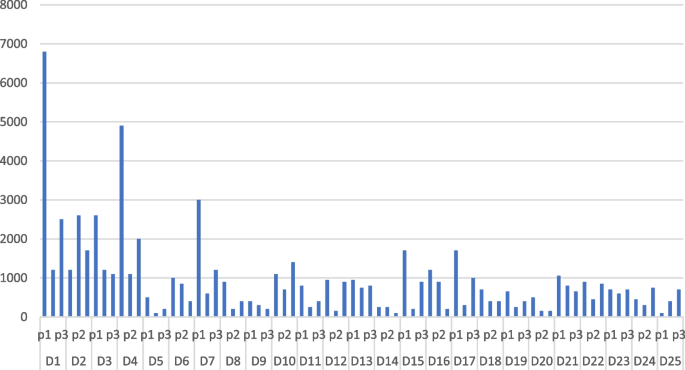
Figure 1 presents the mean daily output, measured in pallets, for each factory across three distinct product types. Additionally, Fig. 2 displays the average daily demand, measured in pallets, for the distribution centers of the same three product types.

Fig. 1

No. of pallets in each source

Fig. 2

No. of pallets in each destination

Results and discussion

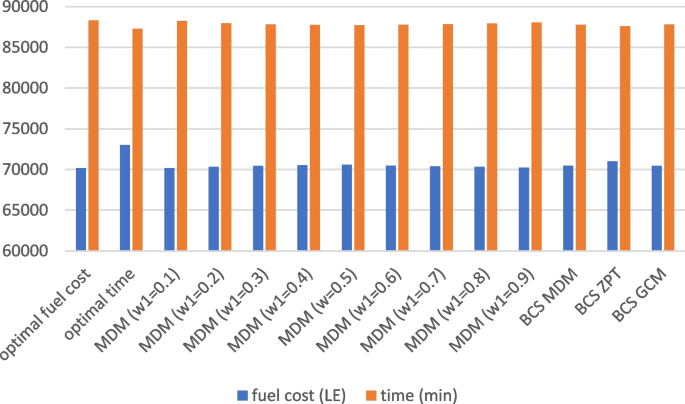
As a result of the case study, the single objective problems of time and fuel consumption cost have been solved. The next step is to prepare a model for the multi-objective multi-dimensional solid transportation problem. Prior to commencing, it is necessary to determine the upper and lower bounds for each objective.

Assuming the first objective is fuel consumption cost and the second objective is time, we calculate the upper and lower bounds as follows:

• The lower bound for the first objective, “cost,” is generated from the optimal solution for its single-objective model, denoted as Z₁(x₁), and equals 70,165.50 L.E.

• The lower bound for the second objective, “time,” is generated from the optimal solution for its single-objective model, denoted as Z₂(x₂), and equals 87,280 min.

• The upper bound for the first objective is obtained by multiplying c_ijkp for the second objective by x_ijkp for the first objective. The resulting value is denoted as Z₁(x₂) and equals 73,027.50 L.E.

• The upper bound for the second objective is obtained by multiplying t_ijkp for the first objective by x_ijkp for the second objective. The resulting value is denoted as Z₂(x₁) and equals 88,286.50 min.

As such, the aspiration levels for each objective are defined from the above values by evaluating the maximum and minimum value of each objective.

The aspiration level for the first objective, denoted as F1, ranges between 70,165.50 and 73,027.50, i.e., 70,165.50 <  = F1 <  = 730,27.50.

The aspiration level for the second objective, denoted as F2, ranges between 87,280 and 88,286.50, i.e., 87,280 <  = F2 <  = 88,286.50.

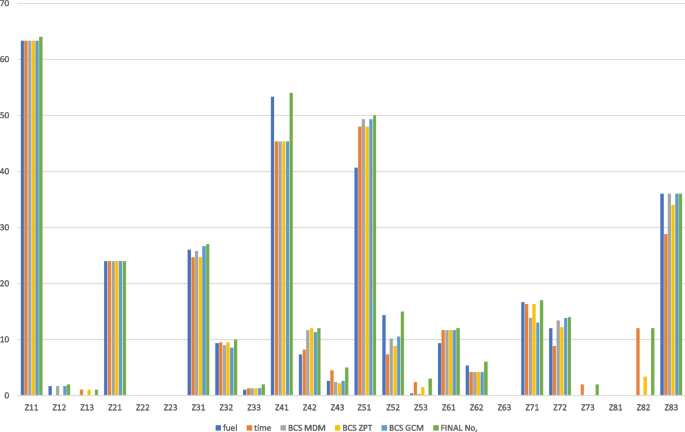
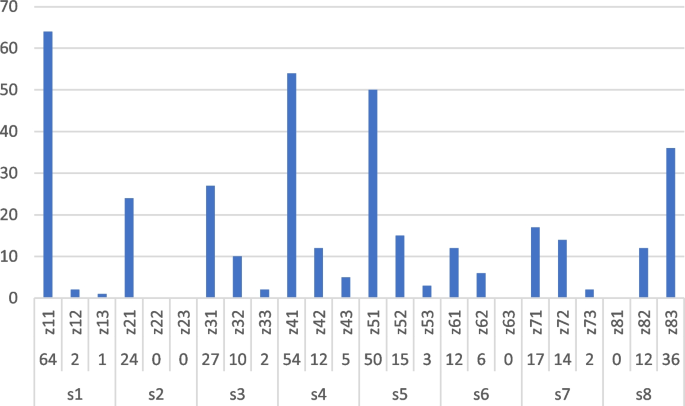
The objective function for the multi-objective multidimensional solid transport problem was determined using the Zimmermann Programming Technique, Global Criteria Method, and Minimum Distance Method. The first two methods directly provided the best compromise solution (BCS), while the last method generated non-dominated extreme points by assigning different weights to each objective and finding the BCS from them. The best compromise solution was obtained using the Lingo software [34]. Table 1 and Fig. 3 present the objective values for the optimal solutions of fuel consumption cost and time, the best compromise solution, and solutions with different weights for both objectives. Figure 4 illustrates the minimum required number of each type of truck for daily transportation of various products from sources to destinations.

Table 1 Objective value in different cases

Fig. 3

Objective value in different cases

Fig. 4

Ideal distribution of the company’s truck fleet

The primary objective of the case study is to determine the minimum number of trucks of each type required daily at each garage for transporting products from factories to distribution centers. The minimum number of trucks needs to be flexible, allowing decision-makers to make various choices, such as minimizing fuel consumption cost, delivery time, or achieving the best compromise between different objectives. To determine the minimum number of required trucks, we compare all the previously studied cases and select the largest number that satisfies the condition: min Zik (should be set) = max Zik (from different cases). Due to the discrepancy between the truck capacity and the quantity of products to be transported, the required number of trucks may have decimal places. In such cases, the fraction is rounded to the nearest whole number. For example, if the quantity of items from a location requires one and a half trucks, two trucks of the specified type are transported on the first day, one and a half trucks are distributed, and half a truck remains in stock at the distribution center. On the next day, only one truck is transferred to the same distribution center, along with the semi-truck left over from the previous day, and so on. This solution may be preferable to transporting trucks that are not at full capacity. Table 2 and Fig. 5 depict the ideal distribution of the company’s truck fleet under various optimization and multi-objective conditions.

Table 2 Ideal distribution of the company’s truck fleet

Fig. 5

Min. No. of trucks should be set for different cases

Conclusions

In conclusion, this research paper addresses the critical issue of optimizing transportation within the context of logistics and supply chain management, specifically focusing on the methods known as the solid transportation problem (STP) and the multi-dimensional solid transportation problem (MDSTP). The study presents a case study conducted on a private sector company in Egypt to determine the optimal distribution of its truck fleet under different optimization and multi-objective conditions.

The research utilizes the multi-objective multi-dimensional solid transportation problem (MOMDSTP) to identify the best compromise solution, taking into account fuel consumption costs and total shipping time. Three decision-making methods, namely the Zimmermann Programming Technique, the Global Criteria Method, and the Minimum Distance Method, are employed to derive optimal solutions for the objectives.

The findings of this study make a significant contribution to the development of approaches for solving multi-objective solid transportation problems with uncertain parameters. The research addresses the complexities of diverse truck fleets and transported products by incorporating fuzzy programming, uncertainty theory, and related concepts. It critically examines the limitations of previous approaches that often focused solely on single-objective solutions and overlooked specific constraints.

The primary objective of this research is to determine the minimum number of trucks required to fulfill decision-makers objectives while optimizing fuel consumption and transportation timeliness. The proposed approach combines the framework of the multi-dimensional solid transportation problem with a multi-objective optimization technique, offering comprehensive solutions for decision-makers with multiple priorities.

This study provides practical solutions for real-world transportation scenarios and demonstrates the potential for enhancing transportation efficiency and cost-effectiveness in various industries or contexts. The comparative analysis of the proposed work highlights the advancements and novelty introduced by the approach, emphasizing its significant contributions to the field of transportation problem research.

Future research should explore additional dimensions of the multi-objective solid transportation problem and incorporate other decision-making methods or optimization techniques. Additionally, incorporating uncertainty analysis and sensitivity analysis can enhance the robustness and reliability of the proposed solutions. Investigating the applicability of the approach in diverse geographical contexts or industries would yield further insights and broaden the potential applications of the research findings.